博古睿讲座17 | 基于概率论的应用数学世界观
基于概率论的应用数学世界观
自牛顿力学作为古典自然哲学出现以来,力学成为了人们对客观世界的科学理解之范式,微积分为其语言,而力成了由运动导致的变化的“外因”。数学里的时间连续性在此有极为重要的角色。不过,在这样的语境里什么是随机性一直是一个令人困惑的问题。不到一百年的概率论的兴起及其应用再次挑战了数学与真实世界之间的关系之话题,重现自古希腊以降到文艺复兴时期一些重大的科学哲学问题。比如:“真理”是怎么来的?什么是随机性?我们到底通过什么样的工具来理解生命现象、理解世界?我们能否基于过去来预测未来?
本次博古睿讲座,美国华盛顿大学西雅图分校应用数学讲座教授钱纮以“基于概率论的应用数学世界观”为题,对以上问题作了回应,并把与概率和求真相关的科学与哲学讨论娓娓道来。钱教授于北京大学获得天体物理学学士学位,于圣路易斯华盛顿大学获得生物化学博士学位。他主要的研究兴趣是生物系统的数学表示与模型,特别是在概率论和统计物理学方面。
北京大学生命科学学院教授白书农老师是本次讲座的与谈人,也是2020-2021博古睿学者,他对生命系统及其演化过程中的随机性十分感兴趣,曾在“白话”专栏中详细讨论。两位老师所作的研究和科普都尝试挑战人类对于“确定性”的常识,并各自从学科角度(生物化学、生物学)给出证据和解释。
力学视域下的世界
在讲座伊始,钱教授用一个案例说明了,预测未来事件发生的概率可能远比我们想象的复杂。
如果我们看这样一串数,“1, 1, 2, 3, 5, 8, 13, ?”,预测后面那个数字是多少,我们可能会发现一个规律是后一个数等于前两个数的和,即13的下一个数应该是21。不过,这一串数也可能是下图这样一个复杂公式的运算结果。这个例子说明,我们对观察到的现象朴素的经验总结很可能是片面的。
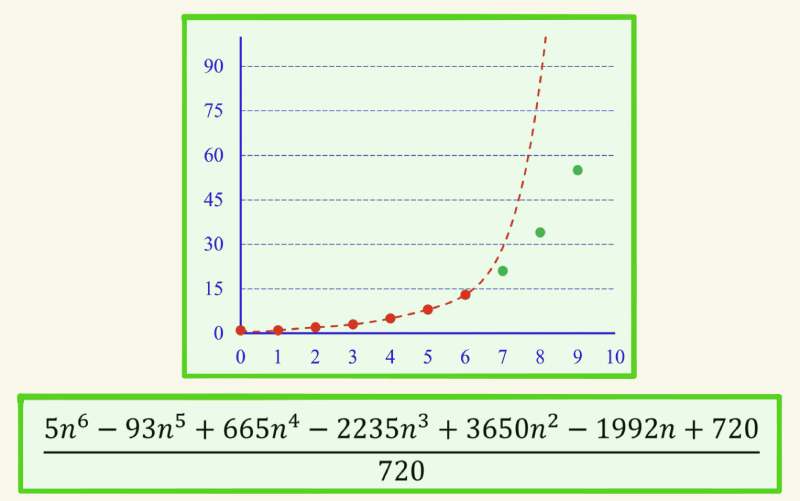
钱教授认为,自牛顿以降,力学成为了解释世界的重要支撑,也成了一种最为基础的科学机理(mechanism)。与之相关的,数学里的时间连续性构成了我们预测事件的要素,正如上面这个案例展示的那样。通过力学的公式化,我们能用微积分把度量世界万物看似最重要的指标——能量——以函数的形式展现出来。如此,无穷复杂的问题变成了一个能量函数,一个函数就能生成无限复杂的世界。能量越大,“活”的越久,能量与时间的连续构成深刻关联。
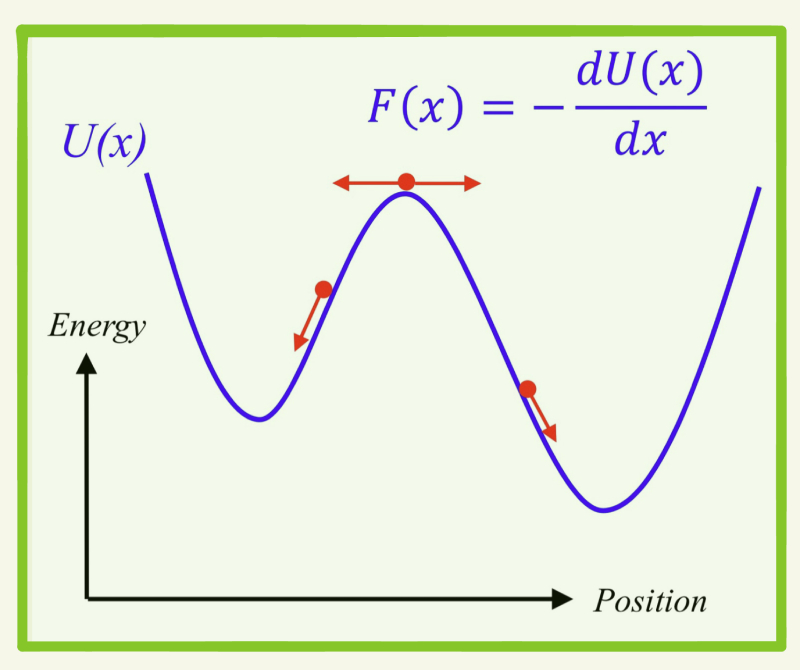
这种理解世界的方式与著名数学家希尔伯特在1900年所提的23个“最重要的数学问题”中第六个问题息息相关,即:物理学理论的数学公理化。对几何学基础的研究也揭示了,虽然物理学并非数学,但是两者之间的关系密切,应该用同样的公理化的方法处理已经大量运用了数学的主要物理学理论框架,在其首位的是关于概率的理论和力学的基础。
不过,通过引用罗杰·彭罗斯,钱教授指出,任何希望使用数学工具的人首先需要搞清楚数学中什么是真的而什么只是假设。意识到理解自然的关键是要基于数学之无可非议可能是人类科学起源的第一个重大突破,但至少到目前,我们离说清楚数学里的“真”,超越一种基于假设的闭环运算,还离的很远。
二十世纪初发展起来的量子力学引进了几率波的物理概念,给力学世界加入了更多元的解释路径。二十一世纪初,有学者甚至提出了带有革命性的新假设:概率论有可能是力学的基础,力学世界的运动和万有引力与概率和熵力相关。那么,到底什么是概率?我们对其能做出什么判断和把握?
频率学派与贝叶斯学派之争
在统计学里对于什么是概率主要有两种主要的观点:概率是一个系统(物体,a body)自己的属性(频率学派);概率是人对世界的一种定量的认识(贝叶斯学派)。
在牛顿的力学框架里,概率所表征的随机性还有另外一个词,所谓“混沌”(chaos)。正如下图所示,一个黑点在一个复杂系统里如何变换、迭代,具有不同的“乱”的程度。在简单系统里,一族点不过是移动位置,稍稍复杂一点的封闭系统中,一族点可能会变成一条线,并且慢慢填满整个方块,但它的面积始终是没变的。再“乱”一点,一个点可以随时变大变小,并集中或离散的出现在方框中的每一个位置,这就是一个开放的“活系统”。
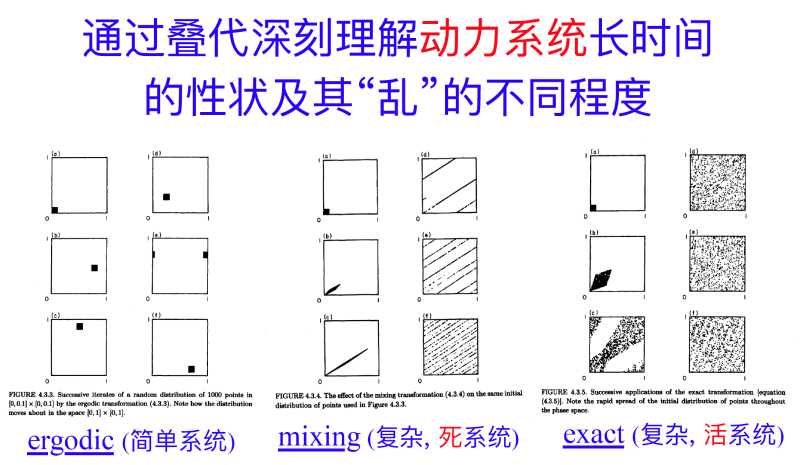
现在的数学家可以对于这几种不同的乱程度,有更系统化的描述。比如,柯尔莫哥洛夫在1934年提出了一种公理化的概率论。他认为,预测未来事件发生的概率,首先需要有一个基本事件的集合,这个集合能够把所有可能发生的情况都囊括进去。
这里存在一个问题,我们怎么可能知道所有可能发生的情况?但是,在牛顿力学体系里,如果我们知道每个原子今天的情况,以后每个原子怎么运动,走到哪里就永远知道了。有同样的思维方式的数学家也证明了对于实数而言,只有有理数和无理数,实数轴上不会存在其他另一种数了。换句话说,如果你相信牛顿力学和这类数学家的判断,那我们的确可以用这个集合了囊括所有的未来事件。

有了集合还不够,预测未来还需要概率测度(probability measure)。我们可以通俗的把概率测度理解成集合中事件所占的权重,每个基本事件都有自己或大或小的比重,影响他们发生的可能。这样,我们就能通过基本事件和他们的概率测度来判断一件事情发生的可能性,从0-1,从绝不会发生到一定发生,预测未来的模型就这么诞生了。
介绍完这种公理化的概率论后,钱教授给了如下的例子来生动的说明不同学派对“概率”的认识:
老张掷一个硬币十次,九次国徽朝上,一次牡丹花朝上。结论是……
小王掷十个一批出厂的硬币,九个国徽朝上,第五个硬币牡丹花朝上。十个结果全部亮在桌面上。概率不复存在!
小王告诉杨老师的结果是九个国徽朝上,一个朝下,但没说是第几个。杨老师于是得出结论是桌面上的每一个硬币都有九比一的概率国徽朝上。
在这个案例里,老张在“频率学派”和“贝叶斯学派”之间徘徊,他不知道到底是硬币头重脚轻决定了这个属性(频率学派的观点),还是他的运气有些极端了,各种复杂因素完全随机地造成了这种状况(贝叶斯学派的观点)。如果老张扔了10000次,结果还9999次国徽朝上,频率学派会更自信地认为这个硬币制造出来是不均的,而贝叶斯学派还是希望避免说这个是硬币自己的特性,因为万一是房间里有风,风导致了这个结果呢?
小王可能是一位应用数学工作者,她信奉柯尔莫哥洛夫理论,所有可能的事件已经在这个实验里发生了。而杨老师可能是一位统计物理学家,他相信对称性和每个硬币完全一样,因此对下一次扔硬币的假想预测还是会基于实验中所有情况加总展现出的概率特性。
物理学、哲学与经济学中的概率与随机性
随着知识的进步,21世纪人们已经对牛顿力学及其相应的概率认识有了很多新的反思。比如力学中,一直有运动学(kinematics)与动力学(dynamics)之分,运动学专注描述运动,不解释运动是如何产生的,这和应用数学很类似,专注于为运动提供数学解释;而动力学则需要解释运动和力以及能量的关系,关注因果,这和理论物理学、哲学有些类似。
在传统的牛顿力学体系中,以加速度为例,a=F/m,F是力,一个外因,一个力使得一个物体有加速度; m是物体的质量,是运动的内因。加速度在这里成为了外因和内因共同作用的“果”。不过当真是这样吗?钱教授介绍,如苏格兰哲学家休谟所言,很多人把一前一后永远一起发生的事件构成因与果,用运动的物体之间的因果关系解释所有的现象,但是这只是一种片面的观察,不能因为我们不断看见一件事情就一定相信他们有因果关系。后来爱因斯坦的研究已经证明了这种力与质量分割在接近光速状态下的不可靠,古典的、朴素的因果关系已经逐渐被近现代的物理学家们点出了局限性。热力学也对牛顿力学的因果识别提出了新的问题:“熵增”指示时间的前后流逝,时间的流逝方向,也就是因果的推导方向。
不仅仅是物理学家,哲学家如笛卡尔、波普尔、库恩都对我们理解随机性和科学中的因果确定作出了突出贡献。也不仅仅是哲学家,经济学家,如凯恩斯,也对概率风险(probability risk)和不确定性(uncertainty)做出了区分——前者是对可能发生事件的测量,而不确定性则完全是我们对未来可能发生事件的一无所知。一个理性人在面对概率风险和不确定性时,做出的行为可能是完全不一样的。
面对这些新的认识,我们或许可以感受到,真正重要的问题已经不是一件事情是否可能,而是它到底有多大的可能会发生。很多事情都可能发生,但只有真正发生了的事情才是事实,对于这种事实,我们不应把它当所理所应当,而是认识到历史中还埋藏着很多“可能性”、“随机性”,这些随机性依旧存在于当下,并完全可能继续影响我们的未来。人可能变成蝴蝶吗?太阳一定从东方升起吗?我们没法给出完全确定的答案,但通过概率,我们能大体作出一种把握。
钱老师进一步指出,概率不是个物体(body)的属性,它是一个运动和变化的系统(动力系统,dynamical system)的一个属性。通过对这种变化系统属性的观测,我们能用统计学的方法得出一定的结论(一套数),从而预测未来各种复杂的状况。但是马克·吐温说任何一套这样的数(统计概率)都是骗人的,因为都隐含着统计者做的假设。
尽管很难把握、并不完备,但是通过把假设说的尽可能清楚,我们还是能求得一定程度上的“真“,并将其用于推进我们对世界的认识。比如,物理学家基于“动力系统”的思维方法,假设一个“周而复始的世界”,其中每个事件都会无穷次地重复,其频率的极限成为概率。
结语
讲座最后,钱老师说,如果我们让一个老智叟和一个小娃娃对话,通过不断机械地问“为什么”,小娃娃一定能逼得老智叟哑口无言。我们当然应当追求真理,但是是否应当“无限”地追求?还是恰当地问“why”, 大胆假设、小心求证,对方法论保持着一种谦卑,对随机性保持一种尊重,对求真保持审慎?这可能需要我们更多地思考。
在问答环节,钱老师和白老师共同探讨了随机性、应用数学与理论物理的关系,并对听众的问题作了建设性的回应。一个有意思的讨论是,如果我们认为所有科学理论都是有假设的,那科学是否也只是认识世界的一种方式,和其他探索并没有深刻差别?我们究竟应当如何对待科学主义,如何对待科学声称是一种更接近“真理”的标准?
两位老师提到,波普尔就把“可证伪性”作为了识别科学的关键一环,科学并不神秘、也不高级,但是它在很多问题上是有处理的优越性的。在一个祖先、宗教、神明皆退场的时代,科学成为了人们更希望托付的对象,成为了让人安身立命、可以自处的一套解释。我们需要科学为我们的生活与实践提供一种“确定性”,让人安心,但也不能忘了历史长河中的“不确定性”与“随机性”。换句话说,对“确定性”的追求是可以理解的,科学在当代也确实提供了一种相对来说不错的解释。但对于到底什么是“真理”,乃至脱离了信仰的“真理”是否存在,我们应当更开放地去问,更包容地去理解,尊重科学,也尊重其他各种重要的知识。
实习生李治霖撰写
简介
活动主办方:
博古睿研究院中国中心
机构
活动时间:
2021-12-04
活动地点:
哔哩哔哩线上直播
活动状态:
已结束
嘉宾











